|
Paul Arsène Xilliez est né le
27 juillet 1868 à Blâmont, fils de Constant Xilliez, employé de
banque, et Marie Clémentine Contois.
Ordonné prêtre le 23 août 1891, il devient, après l'Ecole des
Hautes Etudes, professeur le 1er octobre 1892 à
l'Institution St Pierre Fourier à Lunéville en rhétorique et
philosophie. Le 1er octobre 1894, il redevient élève
à l'Ecole des Carmes à Paris, mais tombe malade à l'été 1895, et
se retire dans sa famille en mars 1896 à Blâmont, où il décède
le 7 octobre 1896, âgé de 28 ans seulement.
Pour d'autres éléments sur sa biographie, voir la
Semaine religieuse du 7 novembre 1896
- n° 45 - p. 887.
.
Pour illustrer les multiples écrits de Paul Xilliez, nous
reproduisons son curieux article sur « La continuité dans la
mémoire immédiate des chiffres et des nombres en série auditive
»
Annales de l'Est
1897
NÉCROLOGIE. - M. L'ABBÉ PAUL
XILLIEZ
La Faculté des lettres vient d'avoir la douleur de perdre un de
ses anciens élèves, M. l'abbé Paul Xilliez, professeur de
philosophie à l'institution B. P. Fourier, de Lunéville, né le
28 juillet 1868, et mort dans sa famille, à Blâmont, le 7
octobre dernier.
M. Xilliez avait été élève de la Faculté pendant l'année
scolaire 1890-1891. Il y suivait les cours préparatoires à la
licence de philosophie. Dès le premier jour, sa simplicité
modeste et distinguée tout à la fois lui avait conquis l'estime
et la sympathie de tous, et ses maîtres, qui avaient bien vite
discerné ses rares qualités d'intelligence, avaient fondé sur
lui les plus sérieuses espérances.
En octobre 1892, l'abbé Xilliez avait été nommé par ses
supérieurs ecclésiastiques professeur à l'institution B. P.
Fourier, de Lunéville. Il devait y rester deux ans et y occuper
successivement la chaire de rhétorique et celle de philosophie.
De son enseignement, qui fut cependant remarqué et très
apprécié, nous ne voulons pas parler ici : nous rappellerons
seulement que c'est lui qui prit l'initiative, - assurément
hardie, aujourd'hui surtout que le vieil édifice de nos lettres
classiques est si vivement battu en brèche - de cette
représentation en grec d'Electre par les élèves de
l'institution, qui réveilla, non sans honneur et sans gloire
pour le collège, le souvenir déjà lointain des « matinées
athéniennes » jadis célèbres des petits séminaires d'Orléans, de
Paris et de Pont-à-Mousson.
A la fin de l'année scolaire 1893-1894, M. Xilliez avait
sollicité un congé de quelques mois qui lui permit, par un
travail personnel plus libre et plus intense, de parfaire encore
sa formation intellectuelle et professorale, et, sur son désir,
en octobre 1894, il échangeait sa chaire de professeur pour une
modeste cellule de l'Ecole des Carmes, à Paris. Ainsi redevenu
étudiant, avec quelle activité débordante n'usa-t-il pas alors
des ressources intellectuelles au sein desquelles sa vie se
trouvait désormais placée ! Les cours et les exercices de la
Sorbonne ne suffisaient pas à son ardeur laborieuse ! Il y
joignait des conférences au Collège de France, à l'École
pratique des Hautes Etudes, à l'Institut catholique, à la
Faculté de théologie protestante, à l'Ecole libre des sciences
politiques. Enfin, l'agrégation de philosophie allait être le
couronnement de ses travaux et de ses études. Admissible en
1895, il avait touché le but de près, et tout lui permettait
d'espérer le succès complet pour le prochain concours. Ce
concours, hélas ! il ne devait pas pouvoir l'affronter. La vie
de labeur excessif qu'il menait depuis quelques mois avait
ébranlé sa santé; un mal implacable s'était déclaré, qui le
minait sourdement. C'est en vain qu'il demande à l'air vivifiant
des cimes alpestres quelque soulagement et quelque espérance.
Une longue cure au sanatorium suisse de Leysin fut impuissante à
conjurer les progrès de la maladie, et, le 7 octobre 1896, il
s'éteignait doucement et pieusement au milieu des siens.
M. l'abbé Xilliez, dans les rares loisirs que lui avait laissés
son enseignement à Lunéville, s'était occupé déjà de la
préparation d'une thèse de doctorat. Son choix s'était porté sur
la philosophie du moyen âge, encore si mal connue en France, et
particulièrement, dans cette période, sur Alexandre de Halès. Il
avait patiemment réuni sur ce sujet de précieux matériaux puisés
à diverses sources, à Paris, à Strasbourg, à Munich, à
Innsbruck, qu'il se proposait de mettre plus tard en oeuvre.
Entre temps, il avait donné aussi à diverses revues, notamment
aux Annales de philosophie chrétienne, dont il était devenu le
collaborateur assidu et apprécié (1), de nombreux articles
critiques remarqués autant pour l'élégante précision de la
forme, que pour la maturité et la vigueur de la pensée (2). Au
commencement de cette année même, l'Année psychologique publiait
de lui une étude très documentée sur la mémoire des chiffres,
résultat d'expériences habilement conduites, sous la
bienveillante direction de M. Binet, au laboratoire de
psychologie physiologique de la Sorbonne (3). Enfin, il y a
quelques mois à peine, sur la chaise longue de malade où la mort
commençait déjà à le serrer de son étreinte, s'aidant
d'observations faites sur lui-même et sur les trop nombreux
compagnons d'infortune qu'il avait rencontrés à Leysin, il avait
entrepris d'écrire, sur le tuberculeux, une étude d'une
psychologie fine et pénétrante, en même temps que d'un charme
plein de tristesse, qu'il destinait au congrès international de
psychologie de Munich, et dont nous avons essayé de sauver les
ébauches (4).
M. Xilliez est mort jeune, alors que les espérances qu'il avait
fait concevoir à ses amis et à ses maîtres allaient devenir des
réalités. Il emporte, dans la tombe prématurée qui se referme
cruellement sur lui, les regrets de tous ceux qui l'ont connu. A
la Faculté des lettres, en particulier, qui lui était restée
chère, et à laquelle il avait voué une affectueuse
reconnaissance, on gardera de lui un souvenir sympathique et
attendri (5).
L. Jérôme.
(1) V. les quelques lignes d'éloge sympathique
que lui a consacrées cette revue, novembre 1896, p. 228-229.
(2) V. en particulier, les articles Métaphysique el sociologie,
dans l'Enseignement chrétien du 16 mars 1895, et l'Obligation
morale et l'idéalisme d'après une thèse récente, dans les
Annales de philosophie chrétienne de juillet 1895. V. aussi
l'Enseignement du 16 décembre 1894, et les Annales de septembre
et novembre 1895, janvier, février, avril, juillet et août 1896.
(3) L'Année psychologique, publiée sous la direction de MM.
Beaunis et Binet. Paris, Alcan, 1896., p. 193-200: La continuité
dans la mémoire immédiate des chiffres et des nombres en série
auditive.
(4) Ce travail, intitulé : La Psychologie du tuberculeux,
paraîtra prochainement dans
la Quinzaine.
(5) V. la notice nécrologique que nous avons consacrée à M.
Xilliez: M. l'abbé Paul Xilliez, professeur de philosophie à
l'institution B P. Fourier de Lunéville, par l'abbé Jérôme,
professeur au grand séminaire de Nancy. Chez Naguer, à Nancy;
in-8° de 20 pages, avec portrait.
Annales de
philosophie chrétienne
Novembre 1896
M. l'abbé XIlliez (1)
Les Annales viennent d'avoir la douleur de perdre l'un de leurs
plus jeunes et de leurs plus distingués collaborateurs. M.
l'abbé Paul Xilliez, professeur licencié de philosophie, ancien
élève du grand séminaire de Nancy et de l'Institut catholique de
Paris, est mort dans la paix du Seigneur, le 7 octobre 1896, à
Blâmont (Meurthe-et-Moselle). Il comptait vingt-huit ans !
Depuis près d'un an il avait
dû interrompre des études qu'il se promettait de couronner par
l'agrégation de philosophie. Déjà proclamé admissible l'année
dernière, ses maîtres et ses amis fondaient les plus sérieuses
espérances sur cet esprit modeste, travailleur, opiniâtre, et
prompt à saisir les côtés difficiles des problèmes de la
philosophie moderne.
Hélas ! un mal implacable lui imposa bientôt de passer l'hiver
et le printemps au Sanatorium de Leysin-sur-Aigle (Suisse).
C'est de cette solitude alpestre qu'il nous envoyait ses
analyses si fines, si justes et si substantielles. Que de fois
on nous a demandé quel était cet auteur à qui chacun était
tenté d'attribuer une longue carrière d'expérience et de savoir
! Dès qu'il connut les Annales, grâce à M. l'abbé Hébert, le
directeur actuel de l'Ecole Fénelon, et qu'il en eut compris le
but, l'esprit scientifique, les tendances exclusivement
philosophiques et apologétiques, il se dévoua généreusement à
leur succès. Nous devons à son talent et à son zèle les
témoignages d'une profonde reconnaissance. Au nom des Annales
nous prions son honorable famille, surtout Madame Xilliez, tant
éprouvée par ailleurs encore, nous prions ses anciens maîtres
d'agréer nos plus vifs sentiments de condoléance.
(1) Une très intéressante notice vient de
paraître sur notre regretté collaborateur; elle est due à la
plume élégante de M. l'abbé Jérôme, professeur au Grand
Séminaire de Nancy. - Chez Vagner, à Nancy, in-8 de 20 pages
avec portrait
L'année
psychologique. v.2
1895
TRAVAUX DU LABORATOIRE DE
PSYCHOLOGIE DE PARIS
LA CONTINUITÉ DANS LA MÉMOIRE IMMÉDIATE DES CHIFFRES ET DES
NOMBRES EN SÉRIE AUDITIVE
L'étude de la mémoire
immédiate des chiffres et des nombres est une source précieuse
d'informations pour le psychologue qui cherche à déterminer les
lois du souvenir. Sans doute, il ne s'agit ici que d'une mémoire
spéciale, à objet strictement déterminé; sans doute encore, il
ne s'agit que d'une reproduction pour ainsi dire mécanique, et
non d'une remémoration proprement dite : on ne saurait dire, en
effet, que le sujet reconnaît les chiffres et les nombres qu'il
répète; il serait plus exact de dire qu'il ne fait que traduire
en états forts les états faibles qui ne sont pas encore effacés
de sa conscience. Mais, si l'étude de la mémoire des chiffres et
des nombres ne permet pas de découvrir les lois de la
reconnaissance, elle peut conduire à la découverte des lois de
la reproduction, ce premier moment du souvenir ; d'autre part,
la comparaison des différentes espèces de mémoires peut conduire
à des lois dont la généralité corrige ce qu'il y avait de trop
spécial dans les résultats des investigations particulières; or,
pour comparer les mémoires, il faut les connaître, et c'est
ainsi que l'étude des différentes mémoires spéciales est la
méthode la plus scientifique pour arriver soit à la confirmation
des lois déjà connues du souvenir, soit à la découverte de lois
nouvelles.
Aussi la mémoire des chiffres et des nombres a-t-elle été, dans
ces dernières années, l'objet de nombreuses recherches.
M. Bourdon (1) a étudié l'influence de l'âge sur la mémoire
immédiate; Münsterberg et Bigham (2), l'influence qu'exerce sur
la mémoire la nature de l'organe sensoriel qui a reçu
l'impression à retenir; Bigham (3), l'influence du temps qu'on
laisse s'écouler entre la perception et la reproduction, la
nature des erreurs commises et la proportion respective des
erreurs par oubli, par déplacement, par substitution, le rang où
les différentes erreurs se produisent le plus fréquemment dans
la série ; Jacobs et Bolton (4), la relation entre
l'intelligence et la mémoire des chiffres; enfin. M. Binet, dans
son intéressante Psychologie des grands calculateurs, a étudié
surtout le mental span et les procédés de calcul des sujets
exceptionnels soumis à ses observations.
Mais il y a, dans cette question de la mémoire des chiffres et
des nombres, un point qui n'a pas encore été examiné, et sur
lequel nous voudrions appeler l'attention des psychologues.
D'une manière générale, il y a dans une série de chiffres ou de
nombres deux choses à considérer : les chiffres ou les nombres,
et les intervalles qui les séparent. Or, on a jusqu'ici étudié
le premier de ces deux éléments, on a négligé presque
entièrement le second. Pourtant l'intervalle a tout autant de
réalité que les termes qu'il sépare, - sinon en lui-même, du
moins dans ce qu'il représente et symbolise, l'effort exigé pour
le franchir. Il est bien plus facile, en effet, de passer de 5 à
6 et de 6 à 7 que de 2 à 9 et de 9 à 5 ; dans le premier cas, on
n'a qu'à se laisser aller à une habitude invétérée; dans le
second cas, il faut lutter contre cette habitude, il faut
contrarier la tendance naturelle que nous avons à garder la
continuité dans la série.
L'idée nous est venue d'étudier cet élément méconnu,
l'intervalle, et de déterminer son influence sur la reproduction
immédiate des chiffres et des nombres en série. Voici, en même
temps que l'indication de la méthode que nous avons suivie,
l'énoncé du principal résultat auquel nous sommes arrivé.
Parlons d'abord des séries de chiffres.
On prononce, devant un sujet attentif, d'un cours de voix à peu
prés uniforme (2 chiffres par seconde) et recto tono, une série
plus ou moins longue de chiffres, en demandant au sujet de les
répéter immédiatement et dans l'ordre même où ils ont été
entendus. On note toutes les réponses très exactement. Il reste
à travailler sur ces matériaux. Appelons intervalle positif
celui qui va d'un chiffre inférieur à un chiffre supérieur; par
exemple, 5 est l'intervalle positif de 2 à 7; appelons
intervalle négatif celui qui va d'un chiffre supérieur à un
chiffre inférieur; par exemple, 3 est l'intervalle négatif de 9
à 6. Or, si nous comparons la somme des intervalles positifs et
négatifs dans la série proposée, et leur somme dans la série
inexacte, nous constatons qu'en général la seconde est
inférieure à la première. Cela montre évidemment que les
erreurs, soit par déplacement, soit par imagination, ne se font
pas au hasard, et qu'il y a une tendance à diminuer les
intervalles, à rétablir la continuité.
Mais il arrive parfois que la série-réponse offre moins de
chiffres que la série proposée. Alors, au lieu de comparer
directement les deux sommes d'intervalles, on divise chacune
d'elles par le nombre des intervalles dont elle est le total, et
on compare les deux quotients. Cette simplification permet
d'opérer sur toutes les séries de chiffres. Supposons, par
exemple, que la série proposée soit : 2, 3, 6, 9, S, 4, 7, 1, et
la série-réponse: 2, 3, 6, 9, 7, 5. Je ne puis évidemment
comparer les deux sommes d'intervalles 21 et 11, puisque les
intervalles ne sont pas en nombre égal dans les deux cas, mais
je puis très bien comparer les quotients de la division de ces
deux sommes parle nombre des intervalles, c'est-à-dire 21/7 et
11/5.
Si nous appelons ces quotients moyennes de discontinuité de la
série, nous pourrons dire alors qu'en général la moyenne de
discontinuité est plus faible dans la série inexacte que dans la
série proposée.
Ce n'est pas tout. Si je veux avoir la moyenne de discontinuité,
non plus seulement pour une série de chiffres, mais pour un
ensemble de séries proposées dans une même expérience, je fais
la somme des valeurs représentant les intervalles, puis celle
des intervalles eux-mêmes; je divise la première somme par la
seconde et j'ai la moyenne de discontinuité de l'ensemble des
séries proposées et celle de l'ensemble des séries inexactes.
Le premier de ces deux quotients ne signifie rien par lui-même,
puisque les chiffres proposés ont été alignés dans un ordre
arbitraire. Au contraire, le second est intéressant, parce qu'il
représente les modifications apportées dans la remémoration.
Nous aurons la valeur numérique exacte de ces modifications, si
nous retranchons le second nombre du premier. En effet, puisque
le premier nombre est le symbole de la discontinuité moyenne
dans les séries proposées, et le second le symbole de la
discontinuité moyenne dans les séries inexactes, leur différence
sera, à son tour, le symbole des changements apportés par la
mémoire dans la discontinuité première. Or, nous l'avons vu, ces
changements se font, en général, dans le sens d'une continuité
plus grande.
Au lieu de porter son attention uniquement sur la somme des
intervalles positifs et négatifs, on peut se demander quel est
le rapport des premiers aux seconds, soit dans une série, soit
dans un ensemble de séries, on peut rechercher si la mémoire
immédiate n'a pas pour l'une ou l'autre des continuités,
ascendante ou descendante, de secrètes préférences. Or il se
trouve que, d'une manière générale, la somme des intervalles
positifs est supérieure à celle des intervalles négatifs.
Mais il est temps d'éclairer par un exemple ces considérations
trop abstraites. Des trois tableaux qui suivent, le premier
représente un ensemble de 20 séries proposées; les deux autres,
les réponses faites par deux sujets différents.
La première colonne après la colonne des séries de chiffres
indique le nombre des chiffres; pour avoir le nombre des
intervalles il suffit de retrancher 1 ; la seconde colonne
indique la somme des intervalles, soit positifs, soit négatifs ;
la troisième, la somme des intervalles positifs; la quatrième,
la somme des intervalles négatifs ; la cinquième, la moyenne de
discontinuité; la sixième, la somme des chiffres de la série.
Pour comparer entre elles les moyennes de discontinuité pour
deux séries complètes d'interrogations, il ne faut évidemment
pas tenir compte des réponses justes : c'est pourquoi nous avons
laissé en blanc la place où elles devraient s'inscrire.
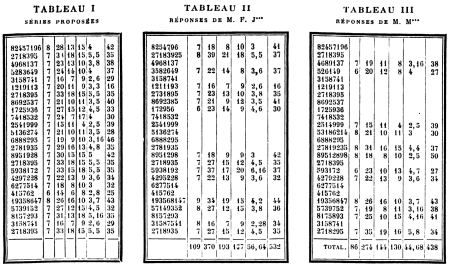
D'après ces tableaux nous avons:

Sur tous les points, les lois que nous avons formulées se
trouvent donc vérifiées.
Dernier problème. La moyenne de discontinuité ne varie-t-elle
pas avec l'âge ? Est-elle la même, par exemple, chez l'enfant et
chez l'adulte ? En aucune façon. L'expérience montre que, chez
les enfants qui apprennent à compter, l'écart est bien plus
grand que chez l'adulte entre la discontinuité des séries
proposées et celle des séries réponses. Les enfants substituent
spontanément à la discontinuité des chiffres ou des nombres la
continuité et surtout la continuité ascendante.
Pour eux, 5 appelle .6 qui, à son tour, évoque 7, et le groupe
567 prévaut facilement contre tout autre groupe discontinu. Des
expériences faites par M. Binet sur les enfants des écoles
primaires de Paris, et dont le savant professeur a bien voulu
nous communiquer les résultats, nous ont permis de vérifier
cette loi, en ce qui concerne les séries de nombres.
M. Binet proposa successivement aux élèves de la 2e classe et
aux élèves plus jeunes de la 5e classe la série suivante:
35, 78, 429, 64, 817.
La somme des discontinuités dans cette série est : 43 + 351+ 325
+ 753 = 1 472. Or, dans la 2e classe, sur 20 séries réponses on
n'en trouve que 5 offrant une somme de discontinuités supérieure
à 1 472. Le total des discontinuités pour l'ensemble des
séries-réponses est de 24 245, ce qui donne une moyenne de 1212,
2 pour chaque série réponse. Or 1212, 2 est inférieur de 259, 8
à 1 472, ce qui confirme la loi énoncée plus haut.
Les réponses de la 5e classe nous en offrent une confirmation
plus frappante encore. Sur 18 séries réponses il n'y en a qu'une
présentant une somme de discontinuités supérieure à 1472. Le
total des discontinuités pour l'ensemble des séries est de 11
565, ce qui donne une moyenne de 642, 5 pour
chaque série. Or 642,5 est inférieur à 1472 de 829,5. Ce dernier
nombre, on le voit, dépasse de beaucoup le nombre correspondant
de la seconde classe.
Un mois après, M. Binet vint faire appel au souvenir des mêmes
élèves, et, sans leur répéter la série primitive, leur demanda
de la reproduire de mémoire. Un certain nombre de réponses
s'approchèrent de la série autrefois proposée : aucune ne la
reproduisit exactement. L'impression première était trop
lointaine, et les traces en étaient à peu près effacées; la
spontanéité imaginative des enfants avait donc libre carrière;
n'étant plus gênée par le rythme sonore et la discontinuité
d'une série dont le souvenir était perdu, elle avait rétabli,
dans une très large mesure, la continuité sériaire. Mais nous
n'insistons pas sur ce point, car c'est ici l'imagination qui
est en jeu, bien plus que la mémoire immédiate. Ce qui parait
assuré, c'est que, chez l'enfant plus que chez l'adulte, on
trouve la tendance à supprimer les discontinuités et à exagérer
la continuité ascendante aux dépens de la continuité
descendante.
Cette loi de continuité a d'ailleurs une relation évidente avec
une loi déjà connue et appliquée à la mémoire : la loi du
moindre effort. La reproduction s'accomplit suivant la ligne de
moindre résistance, et c'est pour cela que la continuité, soit
positive, soit négative, existe plus souvent dans la série
inexacte que dans la série proposée : nous avons contracté, en
effet, l'habitude de nommer les chiffres et les nombres en série
continue, soit ascendante, soit descendante, et cette habitude
générale l'emporte sur les habitudes particulières, ébauchées en
nous par l'audition de chiffres ou de nombres en série
discontinue. Et comme l'habitude de nommer les chiffres et les
nombres en série continue ascendante est plus forte que celle de
les nommer en série continue descendante, la somme des
intervalles positifs est naturellement supérieure à celle des
intervalles négatifs.
Il y a donc un conflit entre l'habitude générale et l'intensité
de la perception remémorée. Tout ce qui fortifie l'habitude
particulière créée par la perception auditive affaiblit
l'habitude générale ; au contraire, toutes les causes qui
favorisent la dissociation des sons entendus, et s'opposent à
leur groupement, laissent par le fait même à la spontanéité
apparente de l'imagination, c'est-à-dire à l'habitude générale,
le loisir de s'exercer sans avoir à lutter contre une habitude
rivale.
S'il fallait une conclusion à ce modeste travail, nous dirions
qu'il apporte une preuve de plus en faveur du déterminisme
psychologique. Les lois de la psychologie ont toute la précision
et toute la rigueur des lois des sciences physiques ; les
exceptions apparentes, si elles ne s'expliquent pas toujours,
parce que certaines circonstances qui les déterminent nous
échappent, s'éliminent cependant et s'annulent quand on
considère un grand nombre de cas. Le caractère d'incertitude et
d'approximation n'appartient qu'en apparence aux lois
psychologiques: ce qui produit cette illusion, c'est la
complexité des faits, c'est la multiplicité des éléments
inconnus qui interviennent dans chaque cas particulier, et dont
l'action est pour nous indéterminable, mais en soi nullement
indéterminée.
Paul Xilliez.
(1) Année psych., I, p. 406.
(2) Année psych., I, p. 411.
(3) Année psych., p. 398.
(4) Mind., XII, p. 45. |













